High-throughput experimentation (HTE) reactors are more and more used in chemical engineering for catalyst screening. The reduction in the size of these fixed-bed catalytic reactors has many advantages, with lower quantities of catalyst and reagents used, better temperature control, minimized safety risks and reduced waste products. Moreover, these reactors can easily be set up in parallel (usually 16 reactors, or more). But despite the many advantages, the behavior of these reactors varies significantly depending on certain parameters (such as the ratio between the diameter of the reactors and that of the particles). It is important to fully understand this type of dependence to ensure optimal operation of the catalytic processes. A PhD thesis led to the definition of a calculation chain capable of accounting for the behavior of these catalysts.
Hydrodynamics governed by preferential paths
The extremely small δ ratio between the diameter of HTE reactors and that of the particles makes it difficult to extrapolate results to bigger scales. In the catalytic beds of these millimetric reactors, particles are arranged non-randomly, resulting in non-uniform radial distributions and higher void fractions. Preferential paths are preponderant and govern the hydrodynamics. The axial behavior of the flow in the reactor is modeled by a 1D convection-dispersion equation. For the latter, the dispersion coefficient with respect to a piston-type flow can be introduced as an axial Péclet1 number.
1 Number comparing convective and diffusive forces
A modeling-based approach
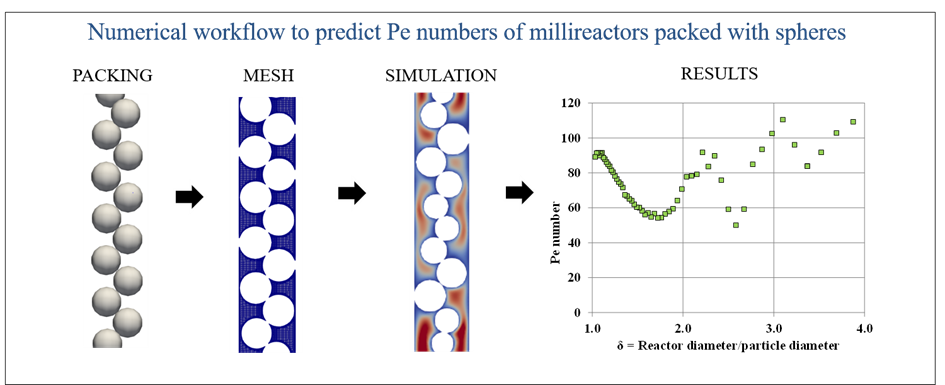
Within the framework of a PhD thesis [1], a fully numerical approach was employed to study the case of single-phase flows in fixed beds of spherical particles with low reactor-sphere diameter ratios (δ < 4). The packing of particles was calculated using the internal Grains3D DEM tool and the OpenFOAM library was used2 to calculate flows and deduce a local Péclet number from the moments of age3.
2 Using the simpleFoam stationary solver, augmented by solving moment of age equations to the second order (See Liu and Tilton, AIChE J. 56, 2010)
3 i.e., from the residence time of fluid particles (first moment), and their variance (second moment)
Possible impacts on process performance
Figure 1 illustrates an important result of this research, namely the reduction in the Péclet number for certain values in the range of low δ ratios, with possible consequences on the catalytic process conversion rate [3]. This can be explained by the formation of ordered arrangements of particles, leading to preferential passages for the fluid and hence less contact time between the fluid and the catalyst.
Simulation results that match reality
In addition, the results obtained from the employed computational workflow compare very favorably with experimental databases [2], particularly when molecular diffusion or superficial velocity vary. The same workflow could be used for other forms of catalyst without additional effort.
References:
[1] V. Petrazzuoli, Impact of packing and porosity filter use in G/S and G/L/S packed bed millireactors:experimental and numerical studies, Thèse de doctorat de l’université de Lyon, soutenue le 02/12/2020.
[2] V. Petrazzuoli, M. Rolland, V.Sassanis, V. Ngu, Y. Schuurman, L. Gamet, Numerical prediction of Péclet number in small-sized fixed bed reactors of spheres, Chemical Eng.ineering Science, 240, 2021.
[3] V. Petrazzuoli, M. Rolland, A. Mekki-Berrada, O Said-Aizpuru, Y. Schuurman, Choosing the right packing in millipacked bed reactors under single phase gas flow, Chemical Eng.ineering Science, 231, 2021.
Scientific contact : lionel.gamet@ifpen.fr
You may also be interested in
In trickle bed reactor simulators, hydrodynamics count!
Improvements in chemical processes are regularly achieved as a result of the introduction of new internal geometries within reactors.
HTE in a milli-fixed bed reactor boosts the development of slurry catalysts
THÈSE DE CHARLES BONNIN
Microfluidics and Chemoinformatics: a highly complementary approach to studying material/fluid compatibility
Pour de nombreuses applications industrielles, comme le recyclage chimique des plastiques, ou encore pour assurer la compatibilité entre polymères et nouveaux carburants, il est essentiel d’anticiper les interactions entre matériaux et fluides...